Heaps

A Heap (aka a Priority Queue) is a data structure that (most commonly) uses a complete binary tree stored in an array, and maintains the heap property so you can repeatedly access the smallest or largest item efficiently.

Core idea

Two rules define a binary heap:

• Complete binary tree: filled level-by-level, left-to-right (last level can be partially filled).
• Heap property:
  • Min Heap: every parent <= its children → smallest element at the top
  • Max Heap: every parent >= its children → largest element at the top

A heap is not fully sorted (unlike a BST). It only guarantees ordering between parent and children.

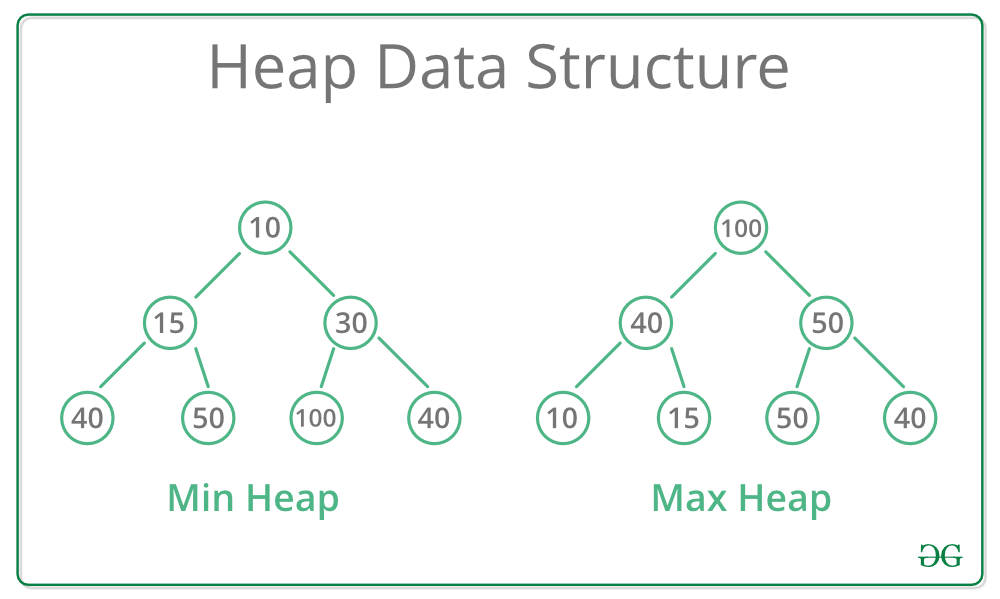
Array representation (why heaps are practical)

Heaps are usually stored in an array A:

• parent(i) = (i - 1) // 2
• left(i) = 2*i + 1
• right(i) = 2*i + 2

This works because the structure is always “complete,” so the tree shape is implicit.

Operations + intuition

• Peek: return the top element (A[0])

  • Time: O(1)

• Insert (push):

  1. append new item to end (keeps completeness)
  2. sift up: while it violates heap property, swap with parent
  • Time: O(log n)

• Pop (extract min/max):

  1. remove the root (this is the answer)
  2. move last element to root
  3. sift down: swap down with the appropriate child until heap property returns
  • Time: O(log n)

Quick example (min-heap)

Start: [2, 5, 3] (valid min-heap)

Insert 1:

• append → [2, 5, 3, 1]
• sift up: swap with 5 → [2, 1, 3, 5]
• sift up: swap with 2 → [1, 2, 3, 5]

Pop:

• remove root 1, move last to root → [5, 2, 3]
• sift down: swap with 2 → [2, 5, 3]

Heapify + build heap (common confusion)

• Heapify (sift-down at an index): fix heap property starting from a node, pushing it down

  • Time: O(log n)

• Build heap from an array (what Python heapq.heapify does): transform an unsorted array into a heap

  • Time: O(n)
  • Extra space: O(1) (in-place)

Heap sort (clarified)

Heap sort is: build a heap, then pop repeatedly to produce sorted output.

• Build heap: O(n)
• Pop n times: O(n log n)
• Total: O(n log n)

(Heaps don’t “heap sort after every pop” — each pop is just O(log n) restructuring.)

Python patterns (heapq)

import heapq
from collections import Counter
from itertools import count
 
# -----------------------------
# Min-heap basics
# -----------------------------
A = [1, 4, 2, 21, 1, 4]
heapq.heapify(A)            # O(n)
 
top = A[0]                  # peek, O(1)
heapq.heappush(A, 4)        # push, O(log n)
minn = heapq.heappop(A)     # pop min, O(log n)
 
# -----------------------------
# Heap sort (ascending)
# Time: O(n log n), Space: O(n) for output
# -----------------------------
def heapsort(arr):
    h = arr[:]              # copy if you want to preserve arr
    heapq.heapify(h)
    return [heapq.heappop(h) for _ in range(len(h))]
 
# -----------------------------
# Max-heap in Python (negation trick)
# -----------------------------
nums = [5, 1, 7, 3]
max_heap = [-x for x in nums]
heapq.heapify(max_heap)
 
maxx = -heapq.heappop(max_heap)
heapq.heappush(max_heap, -10)
 
# -----------------------------
# Priority queue: tuples sort left-to-right
# (priority, value)
# -----------------------------
pq = []
heapq.heappush(pq, (2, "medium"))
heapq.heappush(pq, (1, "urgent"))
priority, value = heapq.heappop(pq)   # (1, "urgent")
 
# -----------------------------
# If value types might not be comparable, use a tie-breaker
# (priority, tie, value)
# -----------------------------
tie = count()
safe = []
heapq.heappush(safe, (1, next(tie), {"job": "x"}))
heapq.heappush(safe, (1, next(tie), {"job": "y"}))
_, _, item = heapq.heappop(safe)
 
# -----------------------------
# Frequency heap: (count, key)
# -----------------------------
D = ["a", "b", "a", "c", "b", "a"]
counter = Counter(D)
 
freq_heap = []
for k, c in counter.items():
    heapq.heappush(freq_heap, (c, k))

Key interview Uses

• Top K: keep a min-heap of size K
• Kth largest: same idea; root is answer after processing
• Dijkstra / A*: min-heap prioritized by current shortest distance
• Merge K sorted lists: heap of current heads

Complexity Cheat Sheet

Operation	Time	Extra Space
Peek	O(1)	O(1)
Push	O(log n)	O(1)
Pop	O(log n)	O(1)
Build heap from array (heapify)	O(n)	O(1)
Heap sort (pop n times)	O(n log n)	O(n) if output list

---

Linked Map of Contexts

Computer Science